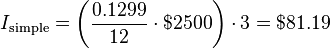Working capital management

Working capital management is the management of the short-term investment and financing of a company.

Liquidity

Liquidity is the ability of the company to satisfy its short-term obligations using assets that are readily converted into cash.

Liquidity management is the ability of the company to generate cash when and where needed.

Liquidity management requires addressing drags and pulls on liquidity.

• Drags on liquidity are forces that delay the collection of cash, such as slow payments by customers and obsolete inventory.
• Pulls on liquidity are decisions that result in paying cash too soon, such as paying trade credit early or a bank reducing a line of credit.
  

Operating and Cash Conversion Cycle

The operating cycle is the length of time it takes a company’s investment in inventory to be collected in cash from customers.

The net operating cycle (or the cash conversion cycle) is the length of time it takes for a company’s investment in inventory to generate cash, considering that some or all of the inventory is purchased using credit.

The length of the company’s operating and cash conversion cycles is a factor that determines how much liquidity a company needs.

The longer the cycle, the greater the company’s need for liquidity.

Management of the Cash Position

Management of the cash position of a company has a goal of maintaining positive cash balances throughout the day.

Forecasting short-term cash flows is difficult because of outside, unpredictable influences (e.g., the general economy).

Companies tend to maintain a minimum balance of cash (a target cash balance) to protect against a negative cash balance.

Examples of Cash Inflows and Outflows
Inflows Receipts from operations, broken down by operating unit, departments, etc. Fund transfers from subsidiaries, joint ventures, third parties Maturing investments Debt proceeds (short and long term) Other income items (interest, etc.) Tax refunds	Outflows Payables and payroll disbursements, broken down by operating unit, departments, etc. Fund transfers to subsidiaries Investments made Debt repayments Interest and dividend payments Tax payments

Working Capital Management

1.      Managing accounts Receivable

• Consider the terms of credit given to customers:
• Ordinary: Net days or, if a discount for paying within a period, discount/discount period, net days (for example, 2/10, net 30).
• Cash before delivery (CBD): Payment before delivery is scheduled.
• Cash on delivery (COD): Payment made at the time of delivery.
• Bill-to-bill: Prior bill must be paid before next delivery.
• Monthly billing: Similar to ordinary, but the net days are the end of the month.
• Consider the method of credit evaluation that the company uses:
• Companies may use a credit-scoring model to make decisions of whether to extend credit, based on characteristics of the customer and prior experience with extending credit to the customer.
  

·         Aging schedule, which is a breakdown of accounts by length of time outstanding:

o   Use a weighted average collection period measure to get a better picture of how long accounts are outstanding.

o   Examine changes from the typical pattern.

·         Number of days receivable:

o   Compare with credit terms.

o   Compare with competitors.

2.      Managing Inventory

• Approaches to managing levels of inventory:
• Economic order quantity: Reorder point—the point when the company orders more inventory, minimizing the sum of order costs and carrying costs.
• Just in time (JIT): Order only when needed, when inventory falls below a specific level
• Materials or manufacturing resource planning (MRP): Coordinates production planning and inventory management.

3.      Managing Accounts Payable

• Factors to consider:
• Company’s centralization of the financial function
• Number, size, and location of vendors
• Trade credit and the cost of alternative forms of short-term financing
• Control of disbursement float (i.e., amount paid but not yet credited to the payer’s account)
• Inventory management system
• E-commerce and electronic data interchange (EDI), which is the customer-to-business payment connection through the internet
  

4.      Managing Short-term Financing

• Characteristics that determine the choice of financing:
• Size of borrower
• Creditworthiness of borrower
• Access to different forms of financing
• Flexibility of borrowing options
• Asset-based loans are loans secured by an asset
  

Transfer Pricing & different Transfer Pricing Methods

Transfer pricing happens whenever 2 companies that are part of the same multinational group trade with each other: when a US-based subsidiary of TATA Group, for example, buys something from a India-based subsidiary of TATA Group. When the parties establish a price for the transaction, this is transfer pricing.

Transfer pricing is not, in itself, illegal or necessarily abusive. What is illegal or abusive is transfer mis pricing, also known as transfer pricing manipulation or abusive transfer pricing.

The Arm’s Length principle

If 2 unrelated companies trade with each other, a market price for the transaction will generally result. This is known as “arms-length” trading, because it is the product of genuine negotiation in a market.  This arm’s length price is usually considered to be acceptable for tax purposes.

But when 2 related companies trade with each other, they may wish to artificially distort the price at which the trade is recorded, to minimize the overall tax bill. This might, for example, help it record as much of its profit as possible in a tax haven with low or zero taxes.

Transfer Pricing Methodology

Following is a short summary of several applicable methods:

• Comparable Uncontrolled Price Method- The comparable uncontrolled price (“CUP”) method compares prices charged in controlled transactions with prices charged in comparable transactions with third parties. Comparable sales may be between two third parties or between one of the related parties and a third party. The CUP method is generally the most reliable measure for arm’s length results, if the transactions are identical or if only minor, readily quantifiable differences exist.
• Resale Price Method- The resale price method (“RPM”) evaluates whether the amount charged in a controlled transaction is at arm’s length, by reference to the gross margin realized in comparable uncontrolled transactions. Under this method, the arm’s length price is measured by subtracting an appropriate gross profit from the applicable resale price of the property involved in the controlled transaction. The resale price method is most often used for distributors that resell products without physically altering them or adding substantial value to them.
• Cost plus Method- The cost plus method compares gross margins of controlled and uncontrolled transactions. Under this method, the arm’s length price is measured by adding an appropriate gross profit to the controlled taxpayer’s cost of producing the property involved in the controlled transaction. The cost plus method is most often used to assess the markup earned by manufacturers selling to related parties.
• Profit Split Method- The profit split method allocates operating profits or losses from controlled transactions in proportion to the relative contributions made by each party in creating the combined profits or losses. Relative contributions must be determined in a manner that reflects the functions performed, risks assumed, resources employed, and costs incurred by each party to the controlled transaction.
• Comparable Profits Method- The comparable profits method (“CPM”) evaluates whether the amount charged in a controlled transaction is at arm’s length by comparing the profitability of one of the parties to the controlled transaction (the “tested party”) to that of companies that are similar to the tested party. The Transactional Net Margin Method (acceptable in Europe and in the OECD guidelines) is a method similar to the CPM.

Basic Business Math

Common Area and Perimeter Formulas

You may need to find out the size of an office space, perimeters of buildings, and tracts of land for your business. Keep these frequently used formulas handy for your business math needs:

Financial Formulas

The most common financial formulas that you need are:

 

Common Business and Financial Acronyms

Important Angle Measures in Degrees

When you’re figuring out things like lot lines or fencing for your business, you’re working with angles. These figures are the more commonly used angle measures and can help you estimate angles for your business tasks:

Financial Option, Foreign Exchange option and Valuation of Foreign Exchange Option

Option is a financial derivative that represents a contract sold by one party (option writer) to another party (option holder). The contract offers the buyer the right, but not the obligation, to buy (call) or sell (put) a security or other financial asset at an agreed-upon price (the strike price) during a certain period of time or on a specific date (exercise date).
Call options give the option to buy at certain price, so the buyer would want the stock to go up.
Put options give the option to sell at a certain price, so the buyer would want the stock to go down.
European option may be exercised only at the expiration date of the option, i.e. at a single pre-defined point in time
American option on the other hand may be exercised at any time before the expiration date
Strike price – the asset price at which the investor can exercise an option
Spot price – the price of the asset at the time of the trade
Forward price – the price of the asset for delivery at a future time
Notional – the amount of each currency that the option allows the investor to sell or buy

A foreign-exchange option or FX option is a derivative financial instrument that gives the right but not the obligation to exchange money denominated in one currency into another currency at a pre-agreed exchange rate on a specified date.
For example a USDINR contract could give the owner the right to sell INR 6,000,000 and buy USD 100,000 on December 31. In this case the pre-agreed exchange rate, or strike price, is 60 INR per USD (or USD/INR 60 as it is typically quoted) and the notional amounts (notionals) are INR 6,000,000 and USD 100,000.

Valuation of a Forex Option: the Garman–Kohlhagen model
Suppose that is the risk-free interest rate to expiry of the domestic currency and is the foreign currency risk-free interest rate (where domestic currency is the currency in which we obtain the value of the option; the formula also requires that FX rates – both strike and current spot be quoted in terms of "units of domestic currency per unit of foreign currency"). The results are also in the same units and to be meaningful need to be converted into one of the currencies.

Then the domestic currency value of a call option into the foreign currency is

 

The value of a put option has value

where :

 

is the current spot rate

is the strike price

is the cumulative normal distribution function

is domestic risk free simple interest rate

is foreign risk free simple interest rate

is the time to maturity (calculated according to the appropriate day count convention)

and is the volatility of the FX rate.

Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. In practice to work out the risk-free interest rate in a particular situation, a risk-free bond is usually chosen that is issued by a government or agency where the risks of default are so low as to be negligible.

The amount of simple interest is calculated according to the following formula:

 

where r is the period interest rate (I/m), B₀ the initial balance and m_t the number of time periods elapsed.

To calculate the period interest rate r, one divides the interest rate I by the number of periods m_t.

For example, imagine that a credit card holder has an outstanding balance of USD2500 and that the simple interest rate is 12.99% per annum. The interest added at the end of 3 months would be,