Financial Option, Foreign Exchange option and Valuation of Foreign Exchange Option



Option is a financial derivative that represents a contract sold by one party (option writer) to another party (option holder). The contract offers the buyer the right, but not the obligation, to buy (call) or sell (put) a security or other financial asset at an agreed-upon price (the strike price) during a certain period of time or on a specific date (exercise date).
Call options give the option to buy at certain price, so the buyer would want the stock to go up.
Put options give the option to sell at a certain price, so the buyer would want the stock to go down.
European option may be exercised only at the expiration date of the option, i.e. at a single pre-defined point in time
American option on the other hand may be exercised at any time before the expiration date
Strike price – the asset price at which the investor can exercise an option
Spot price – the price of the asset at the time of the trade
Forward price – the price of the asset for delivery at a future time
Notional – the amount of each currency that the option allows the investor to sell or buy

A foreign-exchange option or FX option is a derivative financial instrument that gives the right but not the obligation to exchange money denominated in one currency into another currency at a pre-agreed exchange rate on a specified date.
For example a USDINR contract could give the owner the right to sell INR 6,000,000 and buy USD 100,000 on December 31. In this case the pre-agreed exchange rate, or strike price, is 60 INR per USD (or USD/INR 60 as it is typically quoted) and the notional amounts (notionals) are INR 6,000,000 and USD 100,000.

Valuation of a Forex Option: the Garman–Kohlhagen model
Suppose that r_d is the risk-free interest rate to expiry of the domestic currency and r_f is the foreign currency risk-free interest rate (where domestic currency is the currency in which we obtain the value of the option; the formula also requires that FX rates – both strike and current spot be quoted in terms of "units of domestic currency per unit of foreign currency"). The results are also in the same units and to be meaningful need to be converted into one of the currencies.
Then the domestic currency value of a call option into the foreign currency is
 c = S_0e^{-r_f T}\N(d_1) - Ke^{-r_d T}\N(d_2)
The value of a put option has value
p = Ke^{-r_d T}\N(-d_2) - S_0e^{-r_f T}\N(-d_1)
where :
d_1 = \frac{\ln(S_0/K) + (r_d - r_f + \sigma^2/2)T}{\sigma\sqrt{T}} 
d_2 = d_1 - \sigma\sqrt{T}
S_0 is the current spot rate
K is the strike price
N is the cumulative normal distribution function
r_d is domestic risk free simple interest rate
r_f is foreign risk free simple interest rate
T is the time to maturity (calculated according to the appropriate day count convention)
and \sigma is the volatility of the FX rate.
Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. In practice to work out the risk-free interest rate in a particular situation, a risk-free bond is usually chosen that is issued by a government or agency where the risks of default are so low as to be negligible.
The amount of simple interest is calculated according to the following formula:
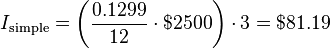
 I_\text{simple} = \left( \frac{0.1299}{12} \cdot $2500 \right) \cdot 3 = $81.19
where r is the period interest rate (I/m), B0 the initial balance and mt the number of time periods elapsed.
To calculate the period interest rate r, one divides the interest rate I by the number of periods mt.
For example, imagine that a credit card holder has an outstanding balance of USD2500 and that the simple interest rate is 12.99% per annum. The interest added at the end of 3 months would be,
I = \left(\frac{0.1299}{12}\cdot $2500\right) \cdot 3 = ($27.0625/\text{month}) \cdot 3=$81.19